data-structure-and-algorithms

代码评价指标：

  1. 算法性能-增效-快：数据结构效率够高，算法是不是够优化
  2. 资源消耗-降本-省：内存够节省

复杂度分析

代码复杂的原因

  1. 不确定性，异常
  2. 资源消耗：时间，CPU，存储，IO
    因此，有效代码的复杂度不能超过某个阈值

O(f(n))：数据量 n ↑，运行代码的行数 f(n) ↑ 的趋势，O order，表示量级。不是真实的数值，而是一个趋势
设，每行代码执行时间相同，则要使算法效率↑，则需要 代码执行时间 ↓ =a*每行代码执行次数 ↓ = b* maxNum(for ↓ ) (a,b>0，代表正比例)
指标优势：不依赖 软硬件性能、数据规模，来估算算法效率

特性：

  1. 只关注最内侧循环中的代码执行次数；同级循环相加；嵌套循环相乘；
  2. 低阶、常量和系数 不左右增长趋势，可以忽略 O(f(n)) + O(g(n))=max(O(f(n)),O(g(n))) O(f(n)) * O(g(n))=O( f(n) * g(n) )

时间复杂度函数

查找 a[n] 中存在i

均摊复杂度

递归

空间复杂度：数据存储空间之外，需要的操作空间

大纲

物理存储方式：同类型批量存储，内存空间连续/不连续，空间连续是数组，空间不连续是链表。数据只有这两种物理存储方式

逻辑存储方式：

访问方式：通过地址访问

基本操作：增删改查

哨兵使用：链表插入删除，字符串处理如KMP模式匹配，二叉树遍历，插入/归并排序，动态规划

由来，特性，解决的问题，使用场景

数据结构

数组 链表

数组 链表
内存空间连续(固定) Y
内存连续，相同数据类型；
- ∈ 线性表，只有前后两个方向
- 按下标寻址，随机访问 O(1)
寻址公式 a[i]=base_address(首地址)+i(偏移量/下标)*data_type_size(数组中每个元素大小)
- 为保证内存连续，增删慢 O(n)，依次移动值
-- 改进：
--- 无序增（新增元素放最后★）
--- 标记删（JVM标记清除★，无内存时删）

 N
节点=数据+指针（空间换时间）。

指针指向下一个节点地址，按指针分类：
- 单链表：tail.next=null
-- 增删 O(1)：abXc->abdc aXbXc->ac
-- 查 O(n)：遍历节点，直到找到
- 双向链表（常用）：pre,next
-- pre即前驱节点，便于前置插入，删除此节点，有序时向前向后查找
-- 常见容器：LinkedHashMap
- 循环链表：last.next = sentinel
-- 用于处理循环结构

头尾节点特殊：
- 头节点记录链表基地址，可遍历得到整个链表；
- 尾节点指向null；
- 哨兵简化头尾节点的特殊处理(减少分支判断)
异常 null ArrayIndexOutOfBounds 访问越界 指针丢失的原因：插入顺序；单链表：1 :p（2:new_node）3：new_node.next=p.next; p.next=new_node;
内存泄漏（C++）：删除节点后，手动释放空间
边界条件：0/1/2/头尾
替代 - ArrayList：封装操作细节，动态扩容；创建时最好指定数组大小★，因为涉及内存申请和数据迁移，比较耗时
- 数组优势：更直观，支持基本类型
VS 插入删除O(n) 随机访问O(1);
连续存储可利用[CPU缓存机制]，预读[数组]中的数据，访问效率更高；
预分配数组值不好确定，copy 耗时如1G		 插入删除O(1) 随机访问O(n);
链表消耗额外存储空间，频繁的内存申请和释放导致频繁的 GC

链表

链表反转：

1
1
2
2
3
3
4
4
5
5
3
3
1
1
2
2
2
2
3
3
4
4
5
5
pre
pre
1
1
next
next
pre.next
pre.next
1
1
3
3
2
2
4
4
5
5
pre: 反转链表中的前一个元素，始终不变
cur=pre.next，反转链表中的第一个元素，反转时节点不更新；但位置变，始终指向下一个要前置的节点
next=cur.next，随cur指向而变
pre: 反转链表中的前一个元素，始终不变...
pre
pre
next
next
cur
cur
cur
cur
pre.next
pre.nextText is not SVG - cannot display 
ListNode cur=pre.next,next=null;  
for (int i = left; i < right; i++) {  
    // 目标：反转一个元素的箭头指向。这个实现过程需改变3个箭头指向
    // print(node.next);  
    next=cur.next;  
    cur.next=next.next;  
    next.next=pre.next;  
    // System.out.println(cur.val+ " "+pre.next.val);  
    pre.next=next;  
    // print(node.next);  
}

栈 队列

栈 队列
进出（操作受限）

操作受限优势：暴露接口少，有天然的约束保障		 1端开放，
节点先进后出 push pop，复杂度O(1)
 排队，节点先进（尾）先出（头）；队尾加元素，队头删元素
数组：head , tail , count , items[capacity]；
- 队空，head=tail；队满，count=items.len
链表：head 哨兵, tail, size, Node(elem,next)
- 队空，head.next=null；
应用 分类：
顺序栈
链式栈

适用：函数调用、
表达式 ★ 求值、
检查表达式中的括号匹配、
浏览器前进后退 ★		 分类：
循环：如db 环形事务缓存
阻塞★(队空队满阻塞)：生产者消费者模型
并发★(多个线程同时操作数据的安全问题：CAS 或者加锁)

适用：资源有限场景 ★：数组队列，请求排队，超长拒绝

栈

JVM中的栈是线程私有的，数据结构更复杂，如帧，局部变量表和操作数栈，专用于方法调用和执行上下文。

池结构或场景，用到队列的排队请求：请求、任务、连接、消息和缓存 的管理

散列表 Hash算法

散列表

扩展于 数组支持用<下标>随机访问的特性 。使用散列函数 hash func，将编号key 映射成数组table index

Hash函数设计

Hash冲突

运动会上，运动员参赛编号

工业级散列表-动态扩容

  1. 散列函数：尽可能散列后的值随机均匀分布，不能太复杂
  2. 装载因子阈值，动态扩容策略：申请新空间，数据搬移到新空间。装载因子0.8，申请2倍空间，则扩容后，装载因子下降到0.4。搬移前，用散列函数重新计算数据位置
    1. 时间复杂度：最好，不需要扩容，O(1)；最坏，O(n)
    2. 如果内存空间大，执行效率要求高，则降低负载因子阈值，相反，增加阈值，甚至可以>1
    3. 渐进式扩容：新数据插入时扩容，新数据放新散列表，并且从老散列表中取1个数据放新散列表；查询时，先从新散列表中查，没有则查老表
  3. 散列冲突
    1. 优先用链表法。也可以将链表改成其他结构，如红黑树，避免O(n)查询；LinkedHashMap
      1. 适合存储大对象，大数据量；更灵活，有支持更多的数据结构
    2. 小规模数据装载因子不高，可用开放寻址 ThreadLocalMap
      1. 优：1. 存放数组，有效利用 CPU 缓存 2. 无指针，序列化简单
      2. 缺：1. 删数据麻烦，标记删除 2. 所有数据在一个数组中，冲突概率大，因此，装载因子阈值要小，内存空间需求大
        HashMap

散列表和链表
散列表，高效操作但无序；链表可以保持顺序

Hash算法

存储 10w 个用户的ID及积分信息，支持，1. 根据id 快速查找、删除、更新积分 2. 查找积分在某个区间的猎头ID列表 3. 按积分小到大，查排名在第 x 位到y位间的猎头ID列表

# 除最底层外，待插入数据所在层面
def generate_level(max_level, p=0.5):
    level = 0
    # <概率，则增加层数
    while random.random() < p and level < max_level:
        level += 1
    return level

// del user
jedis.hdel(USER_HASH_KEY, userId);
jedis.zrem(USER_SCORE_KEY, userId);
// update score
jedis.hset(USER_HASH_KEY, userId, String.valueOf(newScore));
jedis.zadd(USER_SCORE_KEY, newScore, userId);
// select users where score in [minScore, maxScore]
jedis.zrangebyscore(USER_SCORE_KEY, minScore, maxScore);
// sort:score form small to big, select users where user in [start, end] 
jedis.zrange(USER_SCORE_KEY, start, end);

分布式应用

其他应用：网络协议 CRC校验；Git commit id

二叉 红黑树

树

二叉树

A
A
B
B
C
C
D
D
E
E
F
F
G
G
数组存储：A B C D E F G
前序（走到就打印）：A B D E C F G
中序（走完左侧打印）：D B E A F C G
后续（走完右侧打印）：D E B F G C A
数组存储：A B C D E F G前序（走到就打印）：A B D E C F G...Text is not SVG - cannot display

二叉查找树 Binary search tree，快速 增删改查
要求：树中，左子节点值<父节点<右子节点值
查找：while p!=null

散列表 O(1)，二叉查找树

平衡二叉查找树：避免二叉查找树最坏复杂度
左右子树高度差<=1，高度 log2n。完全二叉树√，AVL树√
初衷：解决二叉树退化成链表的问题。平衡指，左右子树高度差尽量小 。红黑树维护成本低，操作性能稳定，高度大约是 log2⁡n
红黑树 read black tree√：最常用的不严格的平衡二叉查找树。
不严格指的是，不满足高度差<=1，但高度稳定的趋近 log2⁡n

  1. 根黑；叶子黑且数据=null
  2. 红色节点的子节点必须黑
    • 因此，红黑树中，红色节点数<黑色节点数
  3. 当前节点，到叶子节点的所有路径中，黑色节点数目相同
    红黑树高度

二叉查找树插入时不需要调整父子节点，所以，一般插入到叶子节点。如果调整父子节点，是因为要保持树的高度平衡，如平衡二叉查找树。
完全二叉树，插入后要调整父子节点，因为数组存储，新节点总是被插入到数组的末尾，需要向上调整父子关系，确保仍满足完全二叉树，即数组存储时，根节点 i=1（下标0空闲）；当前节点的左子节点2i，右子节点 2i+1；反推，已知子节点 i，父节点 i/2。

堆 堆排序

堆

应用
优先级队列：队列先进先出，优先级队列按优先级先出

图 广深优先搜索

图

图

深度和广度优先搜索

BFS(graph, start):
    visited = set()          // 创建一个集合，用于存储已访问过的节点
    queue = Queue()          // 创建一个队列，用于存储待访问的节点

    enqueue(queue, start)    // 将起始节点加入队列
    add visited, start       // 将起始节点标记为已访问

    while queue is not empty:
        vertex = dequeue(queue) // 从队列中取出一个节点

        visit(vertex)           // 访问该节点

        for neighbor in graph.neighbors(vertex): // 遍历该节点的所有邻居
            if neighbor not in visited:
                add visited, neighbor   // 标记邻居节点为已访问
                enqueue(queue, neighbor) // 将未访问的邻居节点加入队列

queue 是一个队列，用于维护待访问的节点，并保持先进先出（FIFO）的顺序。
enqueue(queue, item) 表示将 item 加入到队列 queue 的末尾，而 dequeue(queue) 表示从队列 queue 中移除并返回第一个元素

深度 depth first search：走迷宫，走不通了退回到上个路口，换路，直到找到出口。

DFS(graph, start):
    visited = set()  // 创建一个集合，用于存储已访问过的节点
    stack = []       // 使用列表作为栈

    push(stack, start) // 将起始节点放入栈中
    while stack is not empty:
        vertex = pop(stack) // 取出栈顶元素
        if vertex not in visited:
            visit(vertex)   // 访问节点
            add visited, vertex // 标记为已访问

            for neighbor in graph.neighbors(vertex): // 遍历所有相邻节点
                if neighbor not in visited:
                    push(stack, neighbor) // 如果未访问，则加入栈中，多个邻居加入栈

graph 是表示图的数据结构，可以是邻接表、邻接矩阵等形式
start 是遍历开始的节点
visited 集合用来记录已经访问过的节点，以避免重复访问
stack 是模拟栈操作的列表，用于保存待访问的节点
https://www.hello-algo.com/chapter_graph/graph_traversal/

查找社交网络3度好友关系

字符串

字符串匹配

单模式：在1个串中查找1个串；
BF brute force 暴力匹配

多模式：在1个串中查找多个串
Trie 树，字典树

how, hi, her, hello, so, see
how, hi, her, hello, so, s...
h
h
s
s
i
i
o
o
w
w
e
e
l
l
l
l
o
o
o
o
e
e
e
eText is not SVG - cannot display

算法

思路

递归

计算机擅长重复，人擅长顺序展开

条件

  1. 递推公式：问题A可以拆解成子问题 b c d ，只思考A和直接子问题两层间的关系即可。假设子问题已解决，思考如何解决问题A，抽象成一个公式解决
  2. 终止条件
    注意：

改写成非递归

// 爬楼梯
public int climbStairs(int n) {
    // 特殊情况处理
    if (n == 1) return 1; // 从地面到第一级台阶
    if (n == 2) return 2; // 从地面到第二级台阶
    // 初始化前两个状态（动态规划的简写）
    int prev2 = 1; // dp[1] 从地面到第一级台阶
    int prev1 = 2; // dp[2] 从地面到第二级台阶
    int current = 0;

    // 从第3级台阶开始计算
    for (int i = 3; i <= n; i++) {
        current = prev1 + prev2; // 递推关系
        prev2 = prev1; // 更新 prev2
        prev1 = current; // 更新 prev1
    }

    // 返回到达第 n 级台阶的方法数
    return current;
}

应用：

/**
* actorId：用户ID
* refer_id：推荐人ID
* 改进：添加递归深度；检测环
*/
long findRootReferId (long actorId) {
	Long referId=select refer_id from [table] where actor_id=[actor_id]; 
	if referId=null {
		return actorId;
	}
	return findRootReferId(referId);
}

复杂度分析

递归树：n(h) 和总时间
归并

贪心

greedy
设背包容量100KG，装5种单价和容量不同的豆子，怎么装，背包总价值最大？
按照单价由高到低依次来装

物品 总量kg 总价值元
A 100 100
B 30 90
C 60 120
D 20 80
E 50 75

  1. 一组数据，定义了限制值和期望值，希望从中选出几个数据，满足限制值，期望值最大

    • 限制值 <100kg，期望值 max(总价值)

  2. 当下选择，是限制值相同的条件下，最大期望值数据

    • 重量相同条件下，价值最大。可以通过每一步选择单位重量价值最高的物品来实现

  3. 举例验证结果最优

    • 严格证明结果比较复杂；大部分用贪心解决的问题，正确性是显然成立的
      贪心的答案，不一定是最优解；原因：前面的选择影响后面的选择

  4. 分糖果：m个大小不等的糖果分给n个孩子，m<n，如何分配？转为，从n个孩子中，抽取一部分孩子分配糖果，让每个孩子的满意度最大

  1. 钱币找零：支付K元，有面值1元、5元、10元、50元，100元的纸币，张数分别是 c1、c2、c3、c4、c5，最少用多少张纸币？
  1. 区间覆盖：假设有N个区间，分别是[l1,r1], [l2,r2]...[ln,rn]，选出部分区间，满足两两不相交（端点相交不算），最多能选出多少个区间？
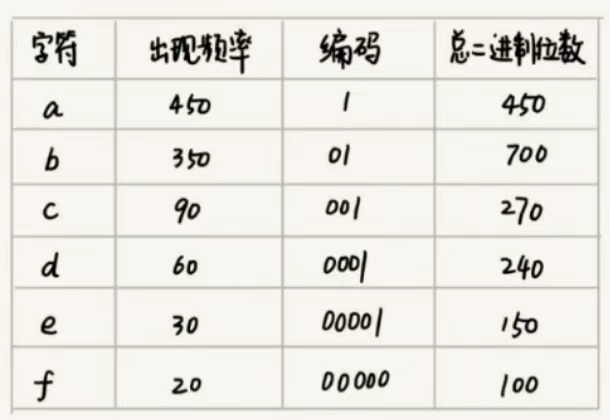
  1. 霍夫曼编码：文件1k字符，每个字符1byte=8bits，存储需要8kbits，找更节省空间的存储方式
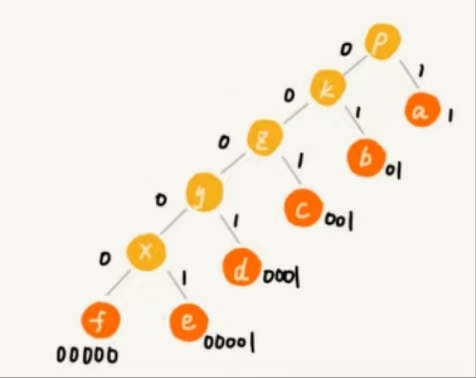
Huffman_Encoding(frequencies):
    priority_queue = PriorityQueue() // 创建一个优先级队列，按照频率排序

    // 将所有字符及其频率作为叶节点加入优先级队列
    for each character, frequency in frequencies:
        node = Node(character, frequency)
        enqueue(priority_queue, node)

    // 循环直到优先级队列中只剩下一个节点
    while size(priority_queue) > 1:
        left = dequeue(priority_queue)  // 取出频率最小的节点作为左子节点
        right = dequeue(priority_queue) // 取出下一个频率最小的节点作为右子节点

        // 创建一个新的内部节点，其频率等于两个子节点频率之和
        new_node = Node('*', left.frequency + right.frequency)
        new_node.left = left
        new_node.right = right

        enqueue(priority_queue, new_node) // 将新节点加入优先级队列

    // 队列中剩下的节点即为霍夫曼树的根节点
    root = dequeue(priority_queue)

    // 使用深度优先搜索来构建霍夫曼编码
    huffman_code = {}
    DFS_Build_Code(root, "")

    return huffman_code

// 深度优先搜索构建霍夫曼编码
DFS_Build_Code(node, code):
    if node is a leaf:
        huffman_code[node.character] = code // 如果是叶节点，则保存编码
    else:
        // 否则递归地对左右子节点进行编码，左子节点添加'0'，右子节点添加'1'
        DFS_Build_Code(node.left, code + "0")
        DFS_Build_Code(node.right, code + "1")

更多应用 ，Prim 和 Kruskal 最小生成树算法，Dijkstra 单源最短路径

分治

MapReduce 的本质是分治。Google MapReduce 在倒排索引，PageRank 计算和网页分析等搜索引擎技术上有大量应用

devide and conquer：大问题化成相同解法的小问题，递归解决问题再合并，每层递归都涉及：

  1. 分解：原问题划为子问题
  2. 解决：递归求解子问题；当子问题足够小，直接求解
  3. 合并：结果合并
    分治算法问题满足：
  4. 原问题可以分成相同算法的子问题
  5. 子问题独立求解，子问题间没有相关性
  6. 分解有终止条件，问题足够小时直接求解
  7. 结果合并的复杂度不能太高，否则无法减少算法的总体复杂度
    应用：
  8. 指导编码，降低问题的复杂度
  1. 海量数据处理

回溯

常用于搜索问题，枚举所有的解，找出满足期望的解
为做到不重不漏，要把问题分成多阶段，每个阶段都会面临一个岔路，随机选择一条走，不通的时候回退到上一个岔路口，走其他的路，必要时剪枝避免搜索所有情况

// template
public void backtrack(参数列表) {
    // 基本情况：如果已经得到了问题的解，那么直接返回或者进行处理
    if (满足结束条件) {
        // 处理解，例如添加到解的集合中
        return;
    }
    
    // 特殊情况：如果当前的尝试不可能产生解，直接返回
    if (不可能产生解) {
        return;
    }

    // 尝试每一种可能的选择
    for (选择的可能选项：选项列表) {
        // 做出选择
        选择；

        // 递归调用，探索做这个选择后的新问题状态
        backtrack(新的参数列表);

        // 撤销选择，回溯
        撤销选择；
    }
}

八皇后

// 主函数
Solve_N_Queens():
    board = create an 8x8 matrix initialized with 0 // 表示棋盘，0表示空格，1表示皇后
    solutions = [] // 存储所有可能的解决方案
    Place_Queens(board, 0, solutions) // 从第0行开始放置皇后
    return solutions

// 放置皇后的辅助函数
Place_Queens(board, row, solutions):
    if row == 8: // 如果已经到达最后一行的下一行，则找到了一个解决方案
        solutions.append(board.copy()) // 将这个解决方案添加到solutions列表中
        return
    
    for col in range(8): // 在当前行尝试每一列
        if Is_Safe(board, row, col): // 检查在[row,col]位置放置皇后是否安全
            board[row][col] = 1 // 放置皇后
            Place_Queens(board, row + 1, solutions) // 递归地放置下一行的皇后
            board[row][col] = 0 // 回溯，移除刚放置的皇后并尝试下一列

// 检查放置皇后是否安全的辅助函数
Is_Safe(board, row, col):
    // 检查同列是否有其他皇后
    for i in range(row):
        if board[i][col] == 1:
            return False

    // 检查左上对角线是否有其他皇后
    for i, j in zip(range(row, -1, -1), range(col, -1, -1)):
        if board[i][j] == 1:
            return False

    // 检查右上对角线是否有其他皇后
    for i, j in zip(range(row, -1, -1), range(col, 8)):
        if board[i][j] == 1:
            return False

    return True // 如果没有冲突，那么放置是安全的

board 是一个二维矩阵，用来表示棋盘的状态
solutions 是一个列表，用于存储所有有效的解决方案
Place_Queens 函数是一个递归函数，它尝试在棋盘的每一行放置一个皇后，并且通过调用 Is_Safe 函数来确保新放置的皇后不会与已放置的皇后相冲突

0-1背包

Knapsack_Optimized(W, weights, values, n):
    // W 是背包的最大容量
    // weights 是一个数组，表示每个物品的重量
    // values 是一个数组，表示每个物品的价值
    // n 是物品的个数

    // 创建一个一维数组 dp，其中 dp[w] 表示当前背包容量为 w 时的最大价值
    dp = array of size (W+1), initialized with 0

    // 填充 dp 数组
    for i from 1 to n: // 遍历物品
        for w from W down to weights[i-1]: // 从后往前遍历所有可能的容量
            if weights[i-1] <= w: // 如果当前物品可以放入背包
                // 尝试放入当前物品，并更新 dp[w] 为最大价值
                dp[w] = max(dp[w], dp[w-weights[i-1]] + values[i-1])

    return dp[W] // 返回 dp 数组的最后一个元素，即为最大价值

使用了一个一维数组 dp 来存储状态。数组的每个位置 dp[w] 表示在背包容量为 w 的条件下能够装入的最大价值。由于每次迭代的状态仅依赖于上一轮迭代的状态，因此我们不再需要二维数组来存储所有的中间状态。关键的优化点是内层循环的遍历顺序。我们从后往前遍历，这样可以确保在计算 dp[w] 时所依赖的状态 dp[w-weights[i-1]] 还未被当前轮次的迭代更新，从而避免了覆盖还未使用的数据。这种方式称为“逆序更新”。这种优化方法假设每个物品只能选择一次（0-1 背包问题的特性）。如果物品可以选择多次，则必须正序更新。

正则表达式匹配

应用：深度优先搜索，编译原理的语法分析，经典数学问题（数独，图的着色，八皇后，0-1背包，旅行商，全排列）

动态规划

动态规划适合求解最优问题，显著降低时间复杂度，提高代码执行效率

为什么需要动态规划？ 大部分动态规划问题可通过回溯算法解决，不过动态规划效率高，用空间换时间。
动态规划问题特征：构建多阶段决策最优解模型，每个阶段对应一组状态，找这组的决策序列使能产生解的最优值

解题思路，

  1. 状态转移表：回溯算法实现-定义状态-画递归树-找重复子问题-画状态转移表-根据递推关系填表-将填表过程翻译成代码
  2. 状态转移方程：找最优子结构-写状态转移方程-将状态转移方程翻译成代码

0-1背包

双十一购物满减，n个商品中选出几个，在满足满(200)减的条件下，怎样最赚？

矩阵最短路径
递推公式 min_dist(i,j)=w[i][j]+min(min_dist(i-1,j),min_dist(i,j-1))

搜索引擎的拼写纠错

最长公共子串长度

算法对比
四个算法都是求最优解，贪心、回溯和动态规划是求多阶段决策，分治不是多阶段

方法

Basic

排序，二分查找

排序算法

升序排序

算法 时间复杂度 基于比较交换 稳定 原地
两个区间：
冒泡、选择；
插入✔、希尔（插入的多区间版）		 O n^2 Y 选择 N Y
多个区间：
快速✔、归并、堆排序		 O nlogn Y 快速 N，堆N
 归并 N
要求特定数据：
桶、计数、基数		 O(n) (线性排序)
O(n+a)，a 是数据范围
O(dn)，d 是维度		 N Y N
稳定：相同的两个数字位置固定

有序度：有序（从小到大）的元素对个数 a[i] <= a(j), if i < j

bubble select insert -> shell
操作 遍历unsort 区间；大值放后面（相邻比较交换） 遍历 unsort 区间，最小放前面（遍历1次找到1个最小值，交换） 向前遍历 sorted 区间，unsort[0]放前面(相邻比较交换)
有序区间在？ 后 前 前
排序比较 交换，需3个动作 非稳定
quick 原地 merge
操作 1. 选择基准分区：小于基准-基准元素-大于基准。基准在最终排序位置上
2. 基准左侧快排，右侧快排
递推公式：quickSort(p..r)=quickSort(p..q-1) + quickSort(q+1..r)；pivot=p；
终止条件：p>=r		 1. 拆分小数组
递推公式：mergeSort(p..r)=merge( mergeSort(p..q) + mergeSort(q+1..r) ), q=p+(r-p)/2；
终止条件：p>=r，小数组内只有一个元素
2. 合并两个有序数组成一个有序数组用：临时数组，再copy 回原数组[p..r]
比较 1. 处理顺序：↓ 向下；分区，处理子问题 1. 处理顺序：↑；处理子问题，合并
图解：
https://www.hello-algo.com/chapter_sorting/quick_sort/
https://www.hello-algo.com/chapter_sorting/merge_sort/
bucket count 基数 radix
操作 数据分m个区间，区内排序，按顺序取出；

分区：len个元素，平均放到 m 个桶，每个桶有元素个数 a= len/m；
- buckets = new int[bucketNum][0]
- 输入 bucketSize,则 m=bucketNum=(maxValue - minValue) / bucketSize + 1

桶内排序：快排		 桶排序的特殊情况：使用中间数组计数，1个值1个组，组内存数值的个数，根据值与顺序和关系排序
-		 稳定算法，从后向前，先按最后一位排序，再按倒数第二位重新排序... 遍历一遍即有序
复杂度 快排复杂度 O(aloga ); m个桶 O(maloga ), ∵ a=len/m，则 m个桶 O(len loglen/m )
when len=m, log len/m = 0，即 O(len)
条件 1. 数据易分成 m 个桶，桶间有大小顺序
2. 数据在桶间数量差不多，否则时间复杂度会高，极端情况退化到 O(nlogn)		 1. 数据范围小
2. 数据是非负整数。其他类型需要转成非负整数		 1. 数据可以分割成独立的位来比较，位间有递进关系，如果高位上，a值>b值，则低位不用比较
2. 每位的数据范围不能太大，可以用线性算法排序
2. 非等长数据，高位补位为0，ASCII中，所有字母>0
适用 1. 外部排序，数据存在磁盘，内存有限无法全部加载
idx 0 1 2 3 4 5 6 7
A[8] 原数组，值是数值 2 5 3 0 2 3 0 3
C[6] 中间数组，计数排序，值是个数 2 0 2 3 0 1
C[6] 排序后顺序求和，值是个数和 2 2 4 7-1 7 8
R[8] 数值在有序数组的存储位置，值是下标 3

通用高性能的排序函数
优化快排：避免退化到 O(n^2)，分区点形成的两个区间，数据量差不多。-> 选分区点

  1. 数据量小1k 2k：归并，使用额外的1k,2k的空间
  2. 数据量大 100M，快排；分区点：三数取中；避免堆栈溢出：堆上实现栈
    1. 快排时排序区间<=4时，用插入 ，插入时用哨兵简化代码（少做1次判断，常用） ；O(n^2)>O(nlogn) 指的增长趋势，但值小时，受常数、系数和低阶函数的影响，n^2可能更小

二分查找

有序查找

二分查找是有序集合的查找算法

// 循环
left = 0
right = length(array) - 1

while left <= right:
    mid = low + (high - low)>>1  // 避免内存溢出，位运算速度更快
    if array[mid] == target:
        return mid  # 找到目标值，返回其索引
    elif array[mid] < target:
        left = mid + 1  # 目标值在右半部分，更新左边界
    else:
        right = mid - 1  # 目标值在左半部分，更新右边界


// 递归
f(left, right) = 
    if array[mid] == target then mid
    else if array[mid] < target then f(mid + 1, right)
    else f(left, mid - 1)

跳表

链表的二分查找，可替代红黑树
实现：加1层索引，查找时遍历的节点数↓
时间复杂度：

这是一个几何级数（geometricseries），其中首项(a=n2)且公比(r=12)。我们知道，对于公比不等于1的几何级数，其前m项和S可以用下面的公式表示：[Sm=a1−rm1−r]在你给出的级数中，最后一项是2，所以我们需要找到m使得(n2m=2)，从而解出m。解这个方程，我们得到：[n=2m+1]现在我们要找m，只需将n除以2，直到结果为2。每次除以2，相当于m增加1。因此，如果我们设(k=m+1)，那么(n=2k)并且(k=log2⁡(n))。现在我们可以计算级数的和：[S=n21−(12)m1−12]代入(m=log2⁡(n)−1)，我们得到：[S=n21−12log2⁡(n)−112][S=n(1−1n/2)][S=n(1−2n)][S=n−2]所以累加和(S)等于(n−2)。

用户积分排行榜

前缀和

双指针

用于线性结构，移动指针，减少不必要的比较和遍历

数组

链表

合并2个数组或链表
数组/字符串，找子序列

用于查找时，和 map 组合，提高效率。

leetcode-287-find-the-duplicate-number

滑动窗口

一种特殊的双指针。都是用2个指针求解。

逻辑：

  1. 初始化：定义两个指针，通常称为left和right，分别代表窗口的左右边界。
  2. 扩展窗口：移动right指针扩展窗口，直到窗口内不满足特定条件。
  3. 收缩窗口：移动left指针收缩窗口，直到窗口内再次满足条件。
  4. 更新结果：在每次窗口满足条件时，根据问题需求更新结果（如最大值、最小值、计数等）。
  5. 重复：重复步骤2和3，直到right指针到达数组或字符串的末尾。

适用于求解：
[最大/最小] + [子数组/子串] 问题：例如，找到最大/最小和子数组、最大/最小乘积子数组等。
连续 [子数组/子串] 问题：例如，找到连续子数组中的最大和、连续子串中不同字符的数量等。
[子数组/子串] 包含特定元素的问题：例如，找到包含所有特定字符的最小子串长度。
滑动窗口内的统计问题：例如，计算滑动窗口内奇数和偶数的数量。

// template
int result = 初始化结果;
int left = 0;

for (int right = 0; right < s.length(); right++) {
    // 扩展窗口
    if (需要收缩窗口) {
        left = 更新left指针;
    }
    // 更新结果
    result = 更新结果;
}

return result;

并查集

了解

数论

计算几何

线性规划

拓扑排序

拓扑排序特别适合依赖关系处理。得到一个合理的执行顺序，确保所有前置任务都在后续任务开始前完成。特别适用于有向无环图。
它是一种线性排序，其目的是对于给定的有向图G=(V, E)，将所有顶点排成一个线性序列，使得对任意边(a, b)∈E，都有a比b先出现在这个序列中。换句话说，对于图中的每一条有向边u->v，顶点u在排序后的序列中都位于顶点v之前。
实现拓扑排序的常用算法包括Kahn算法和基于深度优先搜索（DFS）的算法。Kahn算法的基本思想是反复选择入度为0的节点，将其输出并从图中删除，直到图为空或者找不到入度为0的节点为止；基于DFS的算法则是利用递归回溯的思想，在遍历过程中记录下访问的顺序，最后反转即可得到拓扑排序的结果。

编译器通过分析源文件或配置文件，来获得两个文件间的依赖关系，那如何通过两两关系，确定一个全局的编译顺序呢？
将问题背景，抽象成具体的数据结构：源文件间的依赖关系，抽象成一个有向无环。如何实现拓扑排序？
kahn

检测图中环的存在

最短路径

地图软件计算最优出行路径
有权图，min(边的权重和)

翻译系统，翻译句子，通过翻译单词，返回单词列表，根据可信度选用翻译

位图

网页爬虫中的URL去重

概率统计

过滤垃圾短信

工程中，可以结合三个方法，并且通过具体场景具体测试调整策略，提高判断准确率和召回率（找到所有垃圾短信）

向量空间

音乐推荐系统

B+树

定义问题：限定范围。常见SQL：

索引的B+树，叶子节点是双链表，便于增删时重连节点。

搜索

游戏中的寻路。用A* 搜索算法。
当下是起点，鼠标是终点，在地图中绕过障碍物，找到一条最短路径。
A* 算法是对 Dijkstra 的改造。是一种启发式算法，使用估价函数，贪心的朝着最优可能到达终点的方向前进。

索引

海量数量中快速查找某个数据。如 redis 中的 kv结构。
软件开发本质是对数据的存储和计算。一旦存储数据变多，需要关注存储相关系统的性能，如MySQL，分布式文件系统，消息中间件 MQ。
索引设计

并行

排序：给8G数据排序。排序常用时间复杂度是O(logn)的算法，归并、快速和堆；进一步优化

应用

lib-redis

搜索引擎

一台机器，8G内存，100G硬盘，实现简易搜索引擎

Disruptor

循环有界数组队列
线程间传递消息的内存消息队列，用于 camel, log4j。比 ArrayBlockQueue 性能高一个数量级。
因为机器内存有限，所以有界队列应用更广泛，不可控的因素，会有潜在的风险，极端情况下，无界队列会导致OOM out of memory。
循环队列，避免消息搬移。
当有多个生产者并发往队列里写数据，可能导致数据覆盖丢失；多个消费者消费同一条，可能重复消费。可能解决

  1. 加锁，或CAS优化
  2. 无锁。2阶段写入，写入前加锁，用于申请多个连续的内存空间，则写入无需加锁；
    • 存在的缺点，必须先申请的内存空间先消费

接口鉴权限流

接口鉴权匹配拦截

短链

长网址转成短网址。访问时，重定向到原始网址。
长网址转成短网址：

概念

https://mp.weixin.qq.com/s/om0plD_OuI31ksQHWCjwfw

>>

8的二进制是1000，4的二进制是0100，8>>1=8/21=4，表示右移N位，即/2^N，右移丢弃右侧的位，左边空位填充0。

存储转换

1Byte =8bit
1 KB = 2^10 Byte，500字作文
1 MB = 2^10 KB，50w=500,000汉字
1 GB = 2^10 MB，5亿汉字
1 TB = 2^10 GB，300亿汉字，1000 部电影

210= ，十进制是1024（1k倍），二进制是10 000 000 000；1+10个0，x 2则右移一位
21 = 10（即 2），22 = 100（即 4）

实时统计业务接口中99%响应时间？堆结构

offset

偏移量，如分页查询（fetch,limit）