math-basic-know-geometry
几何->代数
几何
基于实际需要,几何 发展早于 代数
平面几何
发展顺序:感知-定义度量单位-系统书写
感知:
- 农业社会:土地测量计算;通过天狼星升起的角度,确立一年的长度,以确立农时和汛期
- 大规模 城市建设:金字塔建设 知道了 勾股定理和圆周率
定义度量单位:确认 长度和角度的单位
系统书写:如 正多边形 边长和面积的关系;直角三角形和等腰三角形;相似三角形成比例公理体系
基于公理,我们可以拆解问题,解决问题
基本公理:
- 传递 a=b,b=c ->a=c
- 可替 a=b,c=d ->a+c=b+d
- a=b,c=d -> a-c=b-d
- 能彼此重合的图形是全等的
- 整体>部分
几何公理:
- 两点 确立 一条直线 -直线公理
- 有限直线可以延长
- 任意点为心,任意距离 可以画圆 - 圆公理
- 直角相等- 直角公理
- 过线外一点,可仅可做一条平行线
公理是 无理由但合事实的。定理是 基于公理推导出来的结论。
几何证明:对顶角相等
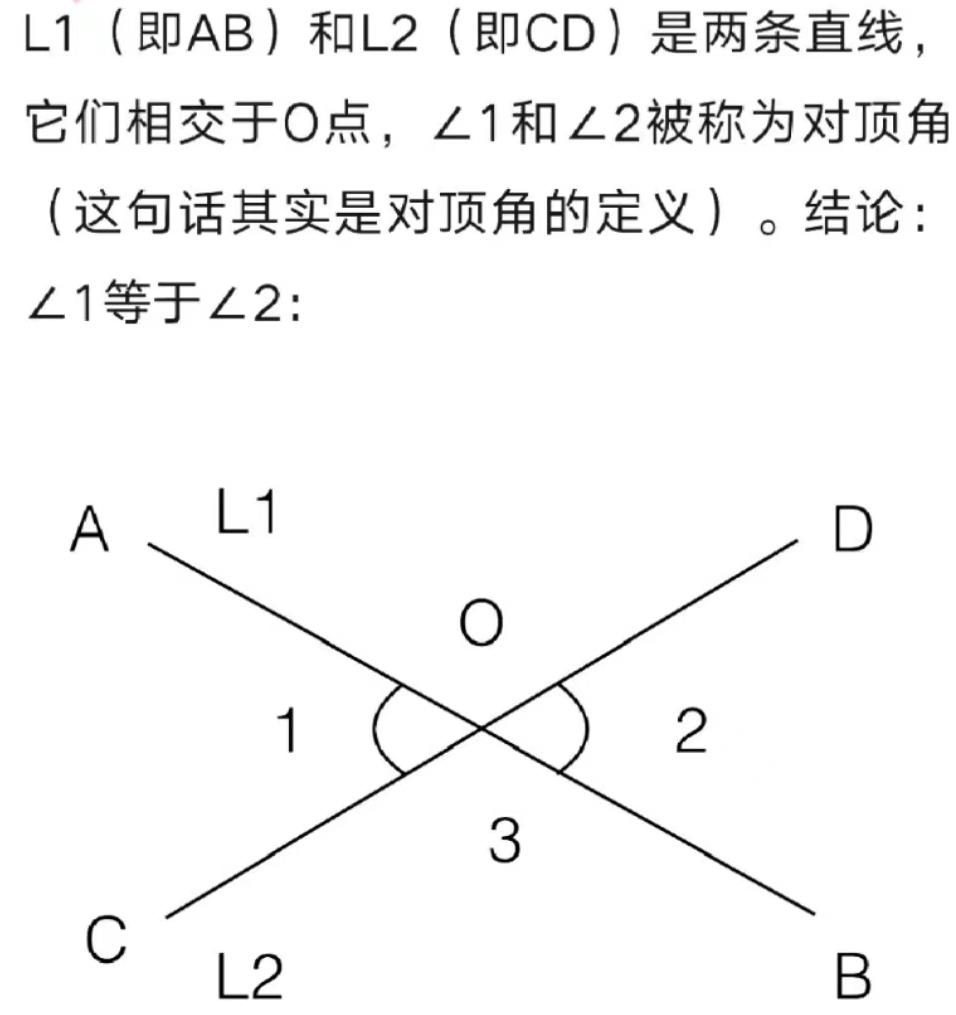
证明:
用定义、公理证明,不引入假设
借用辅助线
定理是基石;定理和一般性问题有区别,一般性问题解决的再多,对体系建设也帮助不大
- 证明引理:所有直线对应角相等
垂直定义:当一条直线L和另一条直线M相交,左右两边夹角相等,则称 M和L 垂直。
直角定义:如果直线 M和L垂直,则夹角就是直角。直角的值=90°
-> 结论:直线的角度=两个直角和
一般公理2:可替,即a=b,c=d ->a+c=b+d
->垂直公理:任意直角相等=90°,任何一条线的角是两个直角相加,
->引理:所有直线的角相等
2. 证明:对顶角相等
引理:∠1+∠3=∠2+∠3
一般公理3:a=b,c=d -> a-c=b-d-> 等式两边-∠3,则 ∠1=∠2
非欧几何
不同于几何公理5(欧式几何),过线外一点,
- 有无数条平行线(罗氏集合) 双曲面,三角和<180°
- 没有平行线(黎曼几何) 椭球空间,三角和>180°
这三个几何工具是等价的。在不同的场景下,有不同的便利之处。比如,非欧几何在球面和曲面上,表达式更简单。一个球面的方程:x^2+y^2+z^2=25,而它在黎曼空间里,方程是 R=5.
爱因斯坦的广义相对论:
一个质量大的物体,会使周围的时空弯曲,万有引力就是弯曲时空的曲率,即时空和物质是相互影响的。E=mc²,能量=质量*光速²。在扭曲的空间里,光线沿着曲线走
解析几何
使用代数方法,解决几何题
直线和方程的关系:
二元一次方程 ax+by+c=0, 在平面方程中代表一条直线,因此这样的二元一次方程也叫线性方程。
一些几何证明题,如定理:三角形三条中线交于一点,用代数方法在坐标系下证明比图形分割组合更容易。
解析几何会让方程解的个数更为直观。
- 二元一次方程组:两条直线交于一点,就是有一个解;两条直线平行,就是没有解;两条直线重合,就是有无数多解。
- 一元二次方程:可能与X轴有一个交点,可能没有,可能两个。
- 一元三次方程:一定与X轴有一个交点,一定有一个解。
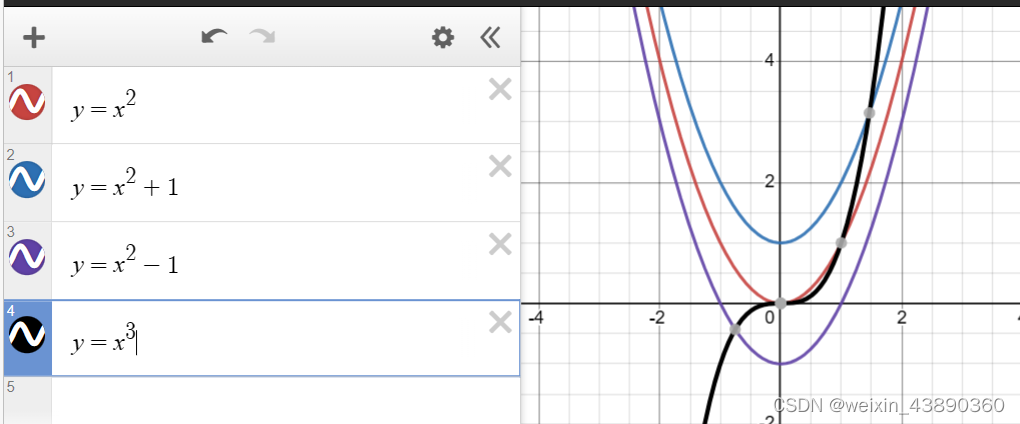
代数
函数
函数反应了变量间的关系
- 变量
- 对应关系
- 对应关系是确定的,即在一个函数中,一个变量只能对应一个值,而不是多个值
- 函数值=对应关系(变量)
函数的出现,让我们从关注 具体的数,变成了关注 趋势。并且可以准确度量趋势的差异
函数也为同一类问题,提供了普遍答案。如,投掷物体的距离=D=V^2×sin2α/g 其中,D表示投掷距离,V表示物体投掷时的抛体速度,α表示抛体与水平面的夹角,g表示重力加速度。 调整初始速度和夹角,可以指导投掷项目的运动员、炮兵和狙击手。
函数的绝对性和变量间的相关性。
- 函数要基于实际,关注定义域。
由自变量推因变量叫函数;由因变量推自变量,叫反函数。两个函数相对45°角的对角线对称
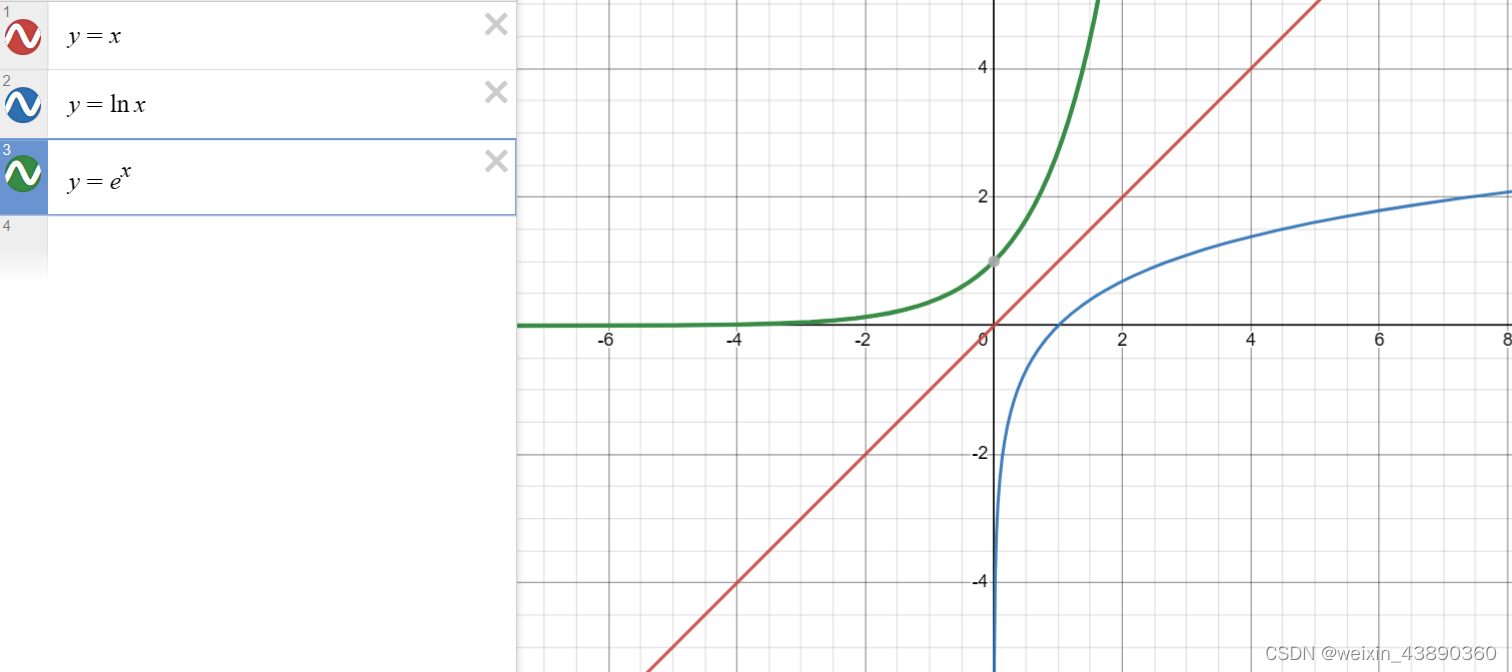
- 自变量共同决定函数值,只能说函数与单个变量间是正相关,但不能说是必然。比如,高风险高回报。
今天的学术研究,只能在几个维度研究相关性,在研究一个变量影响时,只能排除其他变量影响。因此,除了关注研究结论,也要全面看待这个结论。
向量代数
做事方向夹角要尽可能小(合作、方向)、力量尽可能大(专业)
大部分物理量和生活中遇到的数量,不仅要关心数值大小,也要关心其方向。
中心城市,如巴黎,会以凯旋门形成极坐标系,指明 11点钟方向400m;
方形规划城市,如北京,需要以 所在地为原点的直角坐标系,指明东向400m左拐再南向400m;
因此,三维空间,直角坐标系标识向量会更方便。
直角坐标系下,向量长度可以用勾股定理解/余弦函数 解。
向量相加,是两个向量形成平行四边形的对角线的长度。
向量是横着排放的一组数字,每个数字代表一个维度的分量。我们可以用它来算分类,或者说相似性。
- 正交代表无关联
- 两个向量在 各维度的分量 成 比例,则夹角为0。(向量的每个维度叫特征向量)
分类可以是文本分类,可用于简历分类。因此,如果在求职单位有熟人,最好问问职位要求,这样在他们看重的维度你的得分就高,他们不在意的维度,你也不需要强调。
线性代数
多个向量放在一起,形成矩阵。
矩阵计算
M行N列矩阵。可以想象一个公司M个岗位,每个岗位需要N个技能。
设公司是一个跨国公司,它在两个国家的分部分别为 矩阵A,B
- 加法:矩阵相应位置的元素逐个相加
- 乘法:乘加权 后 累加
矩阵的使用,相当于批量处理。
微积分
微分
牛顿求 瞬时速度,使用无限逼近的方法。v(t0)=△S/△t,当△t->0,即某时刻的瞬时速度,就是这个时刻无穷小时间内的平均速度;在坐标系上 表现为 曲线每个点上的切线斜率,也叫导数,导数也是一个函数,反应着原函数变化的快慢。
当一个函数取决于很多变量,用微分的梯度概念,找到最快的方向去努力。
对于不光滑甚至不连续的阶梯函数,在跳跃点是无法计算导数的。当△t->0,△S是一个常数。对于这种情况,我们说函数在这个跳跃点不可导。这个点是一个单独的(不连续的)点,叫奇点。
魏氏证明,连续的光滑的曲线可导。可导有两个条件:连续+光滑(!尖点)。
导数的性质,反映了总量的变化趋势
- 导数>0,原函数↑,导数越大,增幅越快
- 导数<0,原函数↓
- 导数=0,原函数不增不减
积分
速度是距离的微分,距离是速度的积分,两个运算互为逆运算。
从坐标系来看,积分就是求图形的面积。
速度本身是随时间变量的函数,那么距离就需要考虑时刻下的变化,积分可以求出这个变化。
加速度变化先于速度,速度变化先于距离,积分有滞后效应。一旦变化显著,已经是累积了很长时间的了,很难去逆转的。
开车过红灯
设 当前速度 36km/h=10m/s,道路限速 72km/h=20m/s,当距离红绿灯 70m时,黄灯亮起,持续4s变成红灯。
试算,4s内不超速行驶完70m,可以吗,怎么行驶?
- 保持当前速度 10m/s,4s 时间只能行驶 10*4=40m<70m,需要汽车加速行驶。
- 汽车的加速度该是多少呢,假设加速度是一个定值=a m/s²,则
1s后,速度为 (10+a)m/s,即 V(t) = V0 + at
又,最终速度是20m/s,
则 加速时间=10+at=20,t=10/a
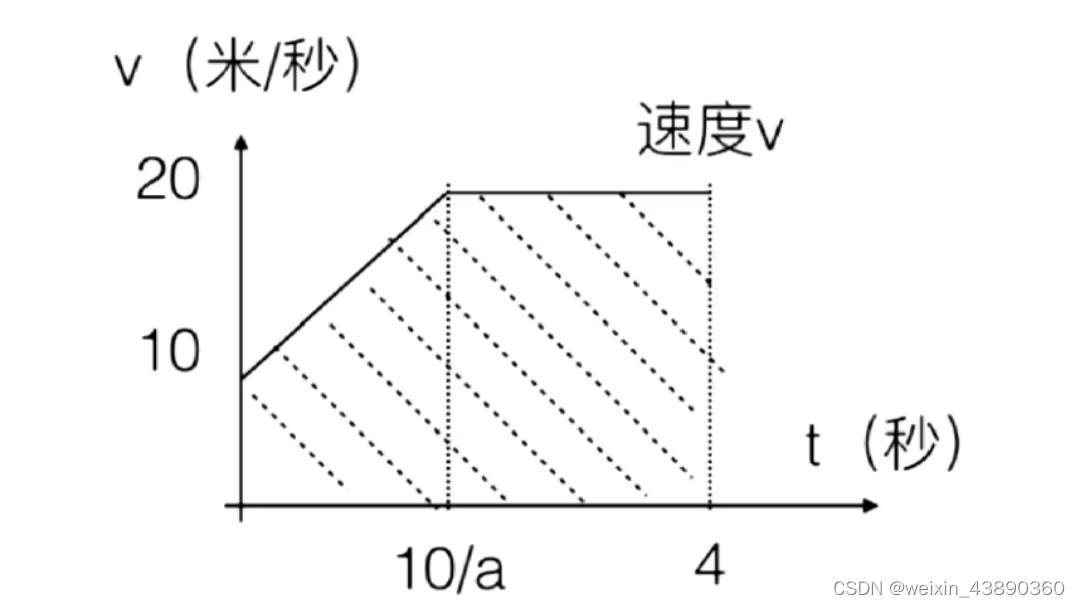
时间-速度函数的面积即为距离。4*20-10*10/a/2=80-50a>70,,则a>5 m/s²
公司营收
两个公司在N个季度里的总营收(单位亿),能通过积分计算出。
N=20,即5年后,
y积分=N*(2+0.2*N)/2=60
z积分 1.1^N/ln1.1(0,20)=60.09
N=19后,
y积分=58
z积分 53.676
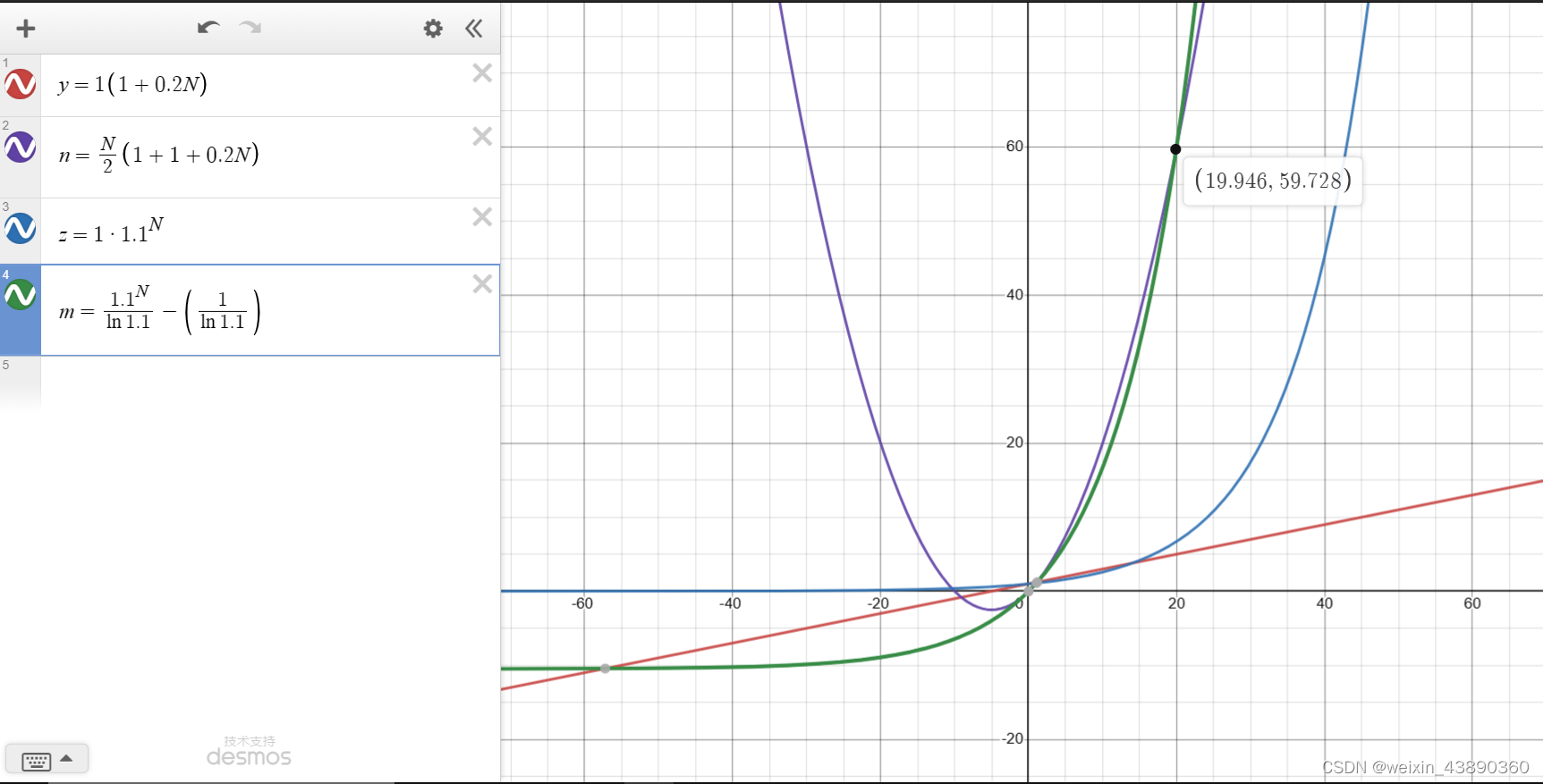
放大看趋势,虽然指数的初始值小的,但变化是快的,长远上,指数更优。
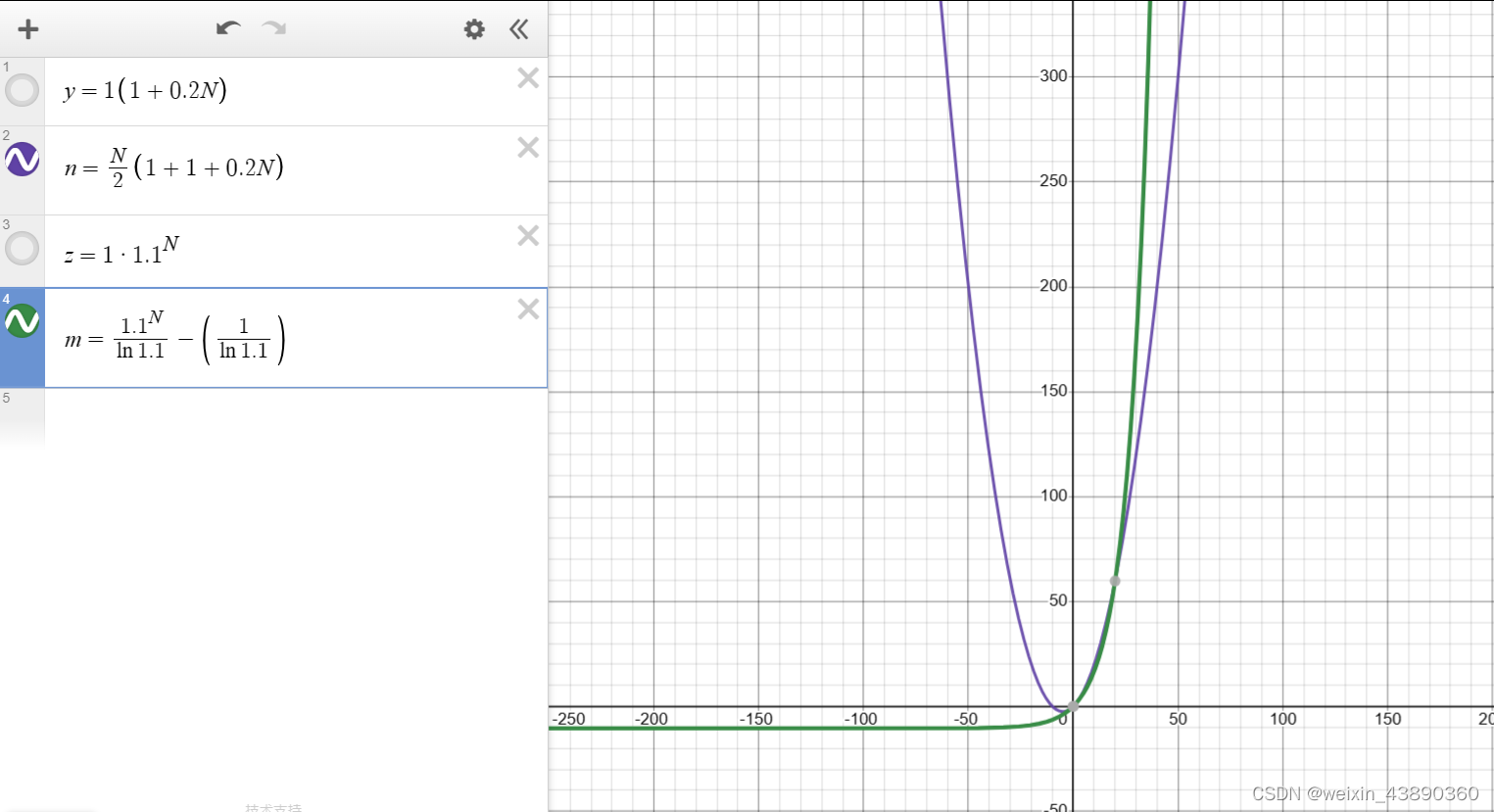
最值
金融上的结构化投资,商业上的博弈论,企业管理上的规划,就是求最值的问题。
求最值方法:
- 有限数集比大小,
- 无限数集求导,导数为0+左右侧符号不同+比较极大值取最值